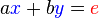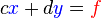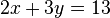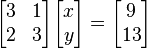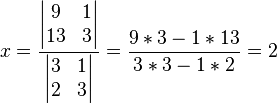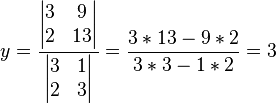miércoles, 26 de noviembre de 2014
4.3.4 Regla de Cramer
La regla de Cramer es un teorema del álgebra lineal que da la solución de un sistema lineal de ecuaciones en términos de determinantes. Recibe este nombre en honor a Gabriel Cramer (1704 - 1752), quien publicó la regla en su Introduction à l'analyse des lignes courbes algébriques de 1750, aunque Colin Maclaurin también publicó el método en su Treatise of Geometry de 1748 (y probablemente sabía del método desde 1729).1
La regla de Cramer es de importancia teórica porque da una expresión explícita para la solución del sistema. Sin embargo, para sistemas de ecuaciones lineales de más de tres ecuaciones su aplicación para la resolución del mismo resulta excesivamente costosa: computacionalmente, es ineficiente para grandes matrices y por ello no es usado en aplicaciones prácticas que pueden implicar muchas ecuaciones. Sin embargo, como no es necesario pivotar matrices, es más eficiente que la eliminación gaussiana para matrices pequeñas, particularmente cuando son usadas operaciones SIMD.
Si 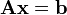 es un sistema de ecuaciones.
es un sistema de ecuaciones.  es la matriz de coeficientes del sistema,
es la matriz de coeficientes del sistema,  es el vector columna de las incógnitas y
es el vector columna de las incógnitas y  es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
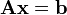 es un sistema de ecuaciones.
es un sistema de ecuaciones.  es la matriz de coeficientes del sistema,
es la matriz de coeficientes del sistema,  es el vector columna de las incógnitas y
es el vector columna de las incógnitas y  es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
donde  es la matriz resultante de reemplazar la j-ésima columna de
es la matriz resultante de reemplazar la j-ésima columna de  por el vector columna
por el vector columna  . Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz
. Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz  ha de ser no nulo.
ha de ser no nulo.
 es la matriz resultante de reemplazar la j-ésima columna de
es la matriz resultante de reemplazar la j-ésima columna de  por el vector columna
por el vector columna  . Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz
. Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz  ha de ser no nulo.
ha de ser no nulo.Sistema de 2x2
Para la resolución de un sistema de dos ecuaciones con dos incógnitas, de la forma. Dado el sistema de ecuaciones:
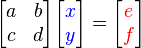
Se representa matricialmente :
Entonces,  e
e  pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:
pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:
 e
e  pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:
pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:Ejemplo
Ejemplo de la resolución de un sistema simple de 2x2:
Dado
que matricialmente es:
x e y pueden ser resueltos usando la regla de Cramer
4.3.3 Propiedades de los Determinantes
PROPIEDADES DE LOS DETERMINANTES.
Los determinantes tienen las siguientes propiedades que son útiles para simplificar su evaluación.
En los párrafos siguientes consideramos que A es una matriz cuadrada.
Propiedad 1.
Si una matriz A tiene un renglón (o una columna) de ceros, el determinante de A es cero.
|
Ejemplo 1.
Sea 

Desarrollando por cofactores del primer renglón se tiene

Propiedad 2.
El determinante de una matriz A es igual al determinante de la transpuesta de A.
|
Esto es
Ejemplo 2.
Sea 


La transpuesta de A es 

Propiedad 3.
Si se intercambian dos renglones (o dos columnas) de una matriz A entonces el determinante cambia de signo.
|
Ejemplo 3.
Sea  con
con 
 con
con
Intercambiando los renglones 1 y 2 la matriz queda
 con
con
Note que los determinantes se calcularon expandiendo por cofactores de la primera columna.
Propiedad 4.
Si una matriz A tiene dos renglones (o dos columnas) iguales entonces det A = 0.
|
Ejemplo 4.
Sea  entonces
entonces 
 entonces
entonces
Propiedad 5.
Cuando un solo renglón (o columna) de una matriz A se multiplica por un escalar r el determinante de la matriz resultante es r veces el determinante de A, r det A.
|
Ejemplo 5.
Sea  cuyo determinante se calculó en el ejemplo 2,
cuyo determinante se calculó en el ejemplo 2, 

 cuyo determinante se calculó en el ejemplo 2,
cuyo determinante se calculó en el ejemplo 2,
Multiplicando el tercer renglón de A por el escalar r = 3 se tiene la matriz B siguiente

cuyo determinante, desarrollado por cofactores de la primera columna de B es
Propiedad 6.
Si un renglón de la matriz A se multiplica por un escalar r y se suma a otro renglón de A, entonces el determinante de la matriz resultante es igual al determinante de A, det A. Lo mismo se cumple para las columnas de A.
|
Ejemplo 6.
Sea  cuyo determinante se calculó en el ejemplo 2,
cuyo determinante se calculó en el ejemplo 2, 
 cuyo determinante se calculó en el ejemplo 2,
cuyo determinante se calculó en el ejemplo 2,
Multiplicando la segunda columna de A por el escalar 2 y sumándola a la columna 3 se obtiene la matriz B siguiente

Expandiendo por cofactores de la primera columna se tiene
Propiedad 7.
Si A y B son matrices de
|
Esto es
Ejemplo 7.
Sean  y
y 
con  y
y 

El producto 
Y su determinante es 
Entonces  .
.
Propiedad 8.
El determinante de la matriz identidad I es igual a 1 (uno)
Ejemplo 8.
I =  det I = (1)(1) – (0)(0) = 1
det I = (1)(1) – (0)(0) = 1
Propiedad 9.
El determinante de una matriz singular, es decir, que no tiene inversa, es igual a 0 (cero)
Ejemplo 9.
J =  |J| = (1)(-12) – (-3)(4) = -12 +12 = 0
|J| = (1)(-12) – (-3)(4) = -12 +12 = 0
Se puede fácilmente comprobar que la matriz J no tiene inversa.
Uso de las propiedades para calcular determinantes de alto orden.
Al utilizar las operaciones elementales sobre renglones, se puede reducir un determinante a una forma mas fácil de evaluar. Si se reduce a una forma triangular superior o inferior, el determinante es el producto de los elementos de la diagonal principal. Al hacerlo hay que tomar en cuenta las propiedades 3, 5 y 6, como en el siguiente ejemplo.
Ejemplo 10.
Calcular el determinante de la matriz A de 

Simplificamos el cálculo del determinante de A reduciendo por renglones

Entonces, la permutación P14 cambia el signo de det A, las operaciones  y
y  no cambian el valor del determinante.
no cambian el valor del determinante.
De esta forma

Se podría seguir reduciendo a la forma triangular, pero observando que hay varios ceros en el tercer renglón resulta fácil desarrollar por cofactores, primero de la primera columna, y después del tercer renglón:

Suscribirse a:
Entradas (Atom)