Reducción de Gauss
El método de Gauss consiste en transformar el sistema dado en otro equivalente. Para ello tomamos la matriz ampliada del sistema y mediante las operaciones elementales por filas la transformamos en una matriz triangular superior ( o inferior ). De esta forma obtenemos un sistema equivalente al inicial y que es muy facil de resolver.
Ejemplo
La matriz ampliada del sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-b4daf9b08947470816a091c908c8b878.png "\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.")
es:
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-9d6156e83361678f19df40db3ecf5638.png "\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)")
Si a la tercera y segunda fila le restamos la primera, obtenemos:
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-45eb9fde313d2a75f1b05cd42aac6c52.png "\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)")
Si ahora intercambiamos la segunda y tercera filas, obtenemos
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-0730ab56aabea929252d49dbf9595acc.png "\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)")
que es la matriz ampliada del sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-eb6ec9bc0f3d4f3655e297c2d80271fe.png "\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.")
que es equivalente al inicial.
Solucionamos la tercera ocuacion para obtener 
:
:
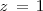
En la primera y segunda ecuación, sustituimos
por la solucion de la tercera ecuación (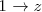 
), para obtener:![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-5c98a4989cffb856e694abe6316e1767.png "\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.")
La segunda ecuación es ahora una ecuación con una sola incognita, 
, que resolvemos para obtener 
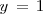. Sustituimos, en la primera ecuación, por 1 (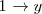 
). Esto nos da una ecuación en 
:
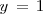, que resolvemos para obtener . Sustituimos, en la primera ecuación, por 1 ( 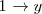). Esto nos da una ecuación en :
que al resolverla termina de darnos la solución del sistema de ecuaciones inicial:
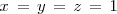
Reducción de Gauss - Jordan
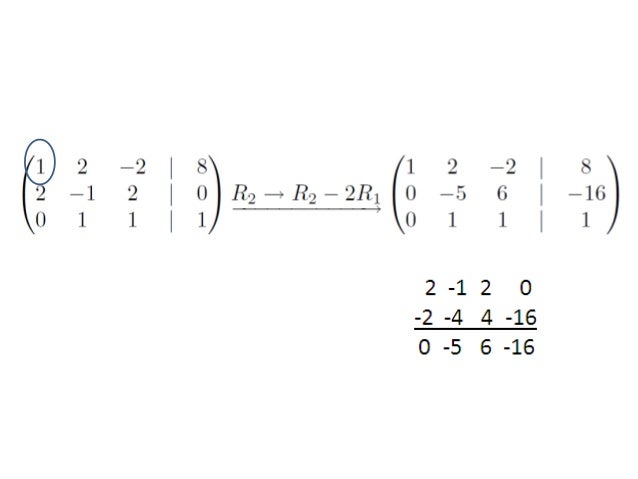
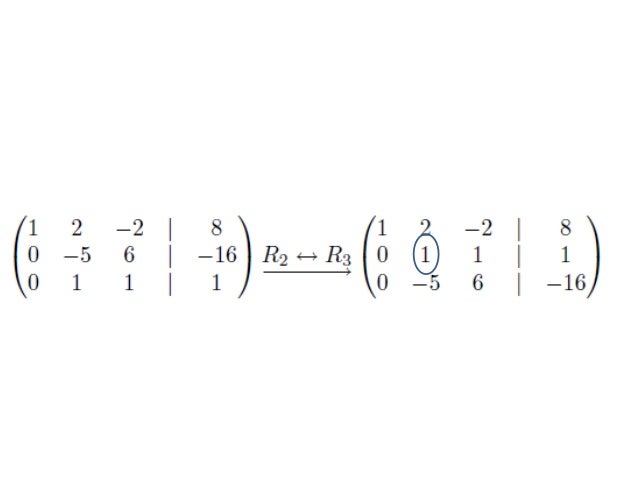
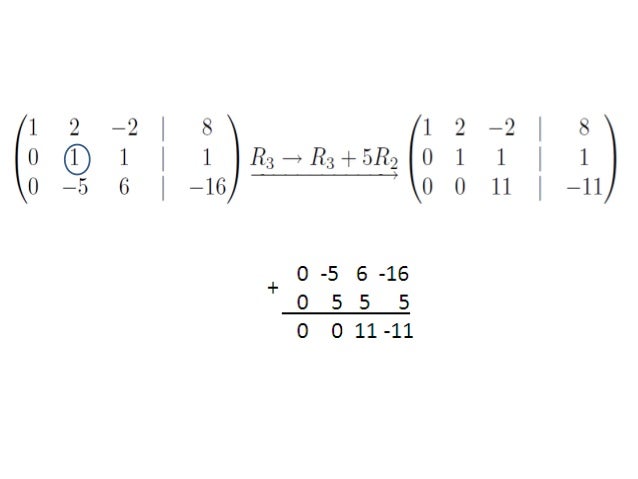
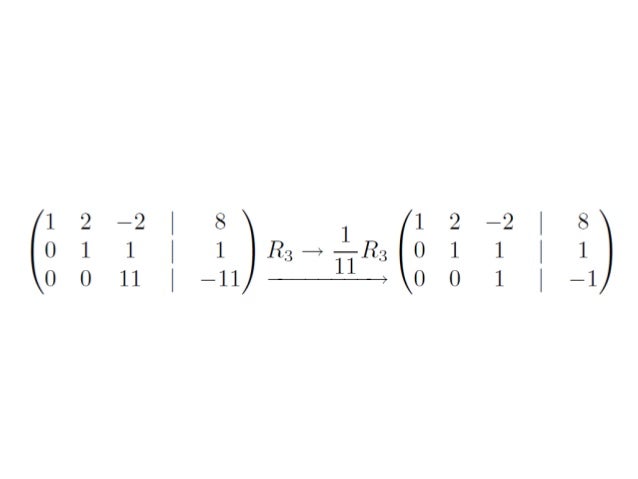
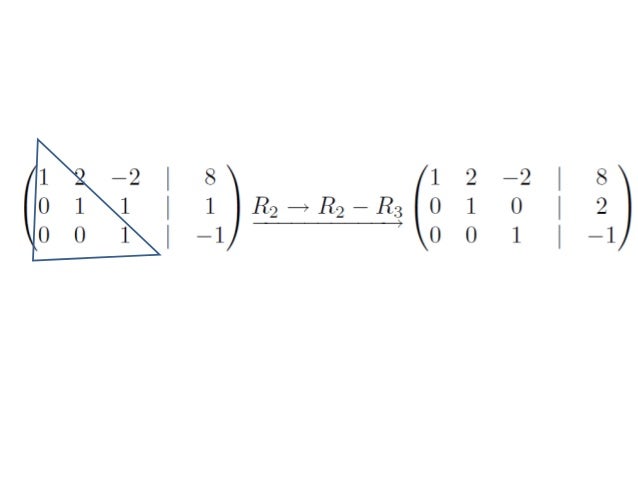
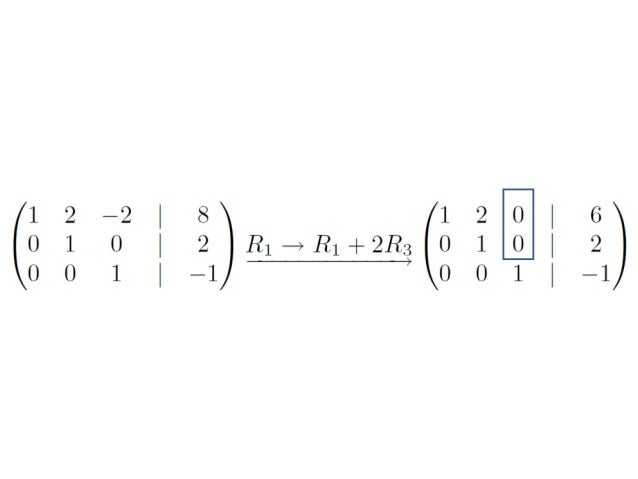
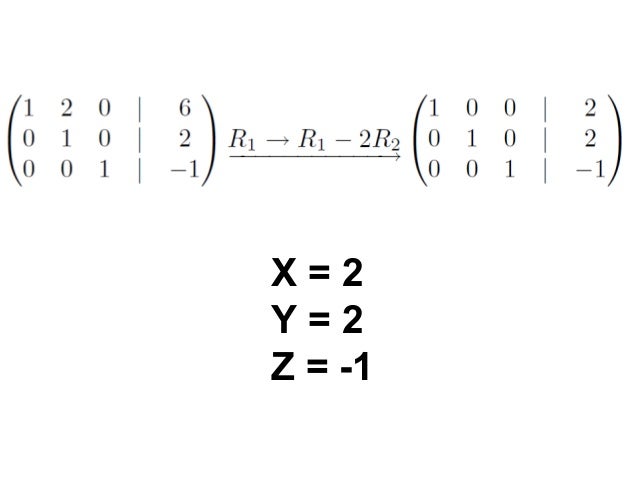
No hay comentarios:
Publicar un comentario